Advertisements
Advertisements
Question
Two boats approaching a light house in mid sea from opposite directions observe the angle of elevation of the top of the light house as 30° and 45° respectively. If the distance between the two boats is 150m, find the height of the light house.
Solution
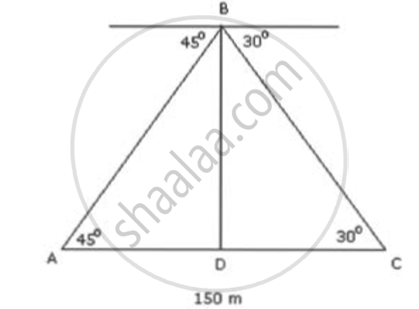
Let the position of the two boats be at points A and C. Let BD be the lighthouse of height h.
Let AD = x. Then, CD = 150 - x
In ΔBAD,
`tan45^circ = "BD"/"AD"`
⇒ `1 = "h"/"X"`
⇒ h = X ...(1)
In ΔBDC,
`tan30^circ = "BD"/"DC"`
⇒ `1/sqrt(3) = "h"/(150 - X)`
⇒ `150 - "X" = sqrt(3)"h"` ....(2)
From (1) and (2),
`150 - "h" = sqrt(3)"h"`
`150 = (sqrt(3) + 1)"h"`
`"h" = 150/(sqrt(3) + 1) xx (sqrt(3) - 1)/(sqrt(3) - 1)`
= `(150(sqrt(3) - 1))/(3 - 1)`
= `75(sqrt(3) - 1)`
= `75 xx 0.732 = 54.9`
Thus, the height of the light house is 54. 9 m.
APPEARS IN
RELATED QUESTIONS
Evaluate without using trigonometric tables.
`2((tan 35^@)/(cot 55^@))^2 + ((cot 55^@)/(tan 35^@)) - 3((sec 40^@)/(cosec 50^@))`
An aeroplane flying horizontally 1 km above the ground and going away from the observer is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°; find the uniform speed of the aeroplane in km per hour.
The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
The angles of depression of two cars on a straight road as observed from the top of a 42m high building are 60° and 75° respectively. Find the distance between the cars if they are on opposite sides of the building.
The angle of elevation of a tower from a point 200 m from its base is θ, when `tan θ = 2/5`. The angle of elevation of this tower from a point 120m from its base is `Φ`. Calculate the height of tower and the value of `Φ`.
Of the two trees are on either side of a river, one of them is 50m high. From the top of this tree the angles of depression of the top and the foot of the other tree are 30° and 60° respectively. Find the width of the river and the height of the other tree.
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
