Advertisements
Advertisements
प्रश्न
Two boats approaching a light house in mid sea from opposite directions observe the angle of elevation of the top of the light house as 30° and 45° respectively. If the distance between the two boats is 150m, find the height of the light house.
उत्तर
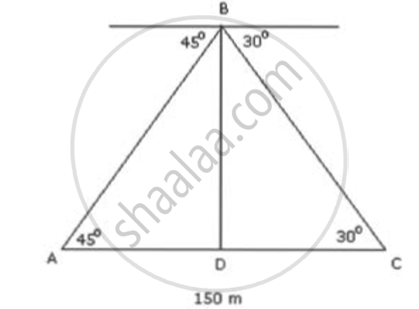
Let the position of the two boats be at points A and C. Let BD be the lighthouse of height h.
Let AD = x. Then, CD = 150 - x
In ΔBAD,
`tan45^circ = "BD"/"AD"`
⇒ `1 = "h"/"X"`
⇒ h = X ...(1)
In ΔBDC,
`tan30^circ = "BD"/"DC"`
⇒ `1/sqrt(3) = "h"/(150 - X)`
⇒ `150 - "X" = sqrt(3)"h"` ....(2)
From (1) and (2),
`150 - "h" = sqrt(3)"h"`
`150 = (sqrt(3) + 1)"h"`
`"h" = 150/(sqrt(3) + 1) xx (sqrt(3) - 1)/(sqrt(3) - 1)`
= `(150(sqrt(3) - 1))/(3 - 1)`
= `75(sqrt(3) - 1)`
= `75 xx 0.732 = 54.9`
Thus, the height of the light house is 54. 9 m.
APPEARS IN
संबंधित प्रश्न
A man in a boat rowing away from a lighthouse 150 m high, takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 45°. Find the speed of the boat.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
Find AD.

Calculate AB.

An aeroplane, at an altitude of 250 m, observes the angles of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. If the boats are on the opposite sides of the aeroplane, find the width of the river. Write the answer correct to the nearest whole number.
The top of a ladder reaches a pcint on the wall 5 m above the ground. If the foot of the ladder makes an angle of 30° with the ground, find the length of the ladder.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
An observer, 1.5m tall, is 28.5m away from a tower 30m high. Determine the angle of elevation of the top of the tower from his eye.
From a point 10 m above the ground , the angle of elevation of the top of a tower is α and the angle of depression is β . If tan α = `5/2` and tan β = `1/4` , calculate the height of the tower to the nearest metre .
An aeroplane at an altitude of 250 m observes the angle of depression of two Boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
