Advertisements
Advertisements
प्रश्न
A man in a boat rowing away from a lighthouse 150 m high, takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 45°. Find the speed of the boat.
उत्तर
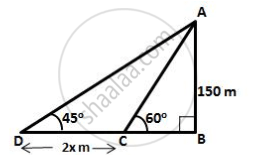
Let AB be the lighthouse and C and D be the two positions of the boat such that AB = 150 m, ∠ADB = 45° and ∠ACB = 60°.
Let speed of the boat be x metre per minute.
Therefore, CD = 2x m;
In ΔADB,
`(AB)/(DB) = tan 45^circ`
`=>` BD = 150 m
In ΔABC,
`(AB)/(BC) = tan 60^circ = sqrt(3)`
`=> 150/(BC)= sqrt(3)`
`=> BC = 150/ sqrt(3)`
= `150/1.732`
= 86.605 m
∴ CD = BD – BC
= 150 – 86.605
= 63.395 m
`=>` 2x = 63.395
`=> x = 63.395/2`
= 31.6975 m/min
= `31.6975/60` m/sec
= 0.53 m/sec
Hence, the speed of the boat is 0.53 m/sec
APPEARS IN
संबंधित प्रश्न
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is 30° and 24° respectively.
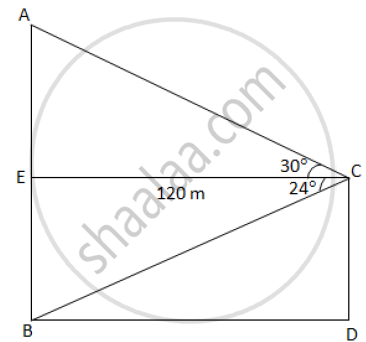
Find the height of the two towers. Give your answer correct to 3 significant figures
The radius of a circle is given as 15 cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, calculate:
- the length of AB;
- the distance of AB from the centre C.
A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole is 60° and the angle of elevation of the top of the pole, as seen from the foot of the tower is 30°. Find:
- the height of the tower;
- the horizontal distance between the pole and the tower.
A kite tied to a string makes an angle of 60° with the ground. Find the perpendicular height of the kite if the length of its string is 250 m.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
A man on the top of a tower observes that a car is moving directly at a uniform speed towards it. If it takes 720 seconds for the angle of depression to change from 30° to 45°, how soon will the car reach the observation tower?
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
