Advertisements
Advertisements
प्रश्न
A man on the top of a tower observes that a car is moving directly at a uniform speed towards it. If it takes 720 seconds for the angle of depression to change from 30° to 45°, how soon will the car reach the observation tower?
उत्तर
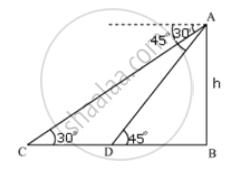
Let AB be the tower .
Initial position of car is C , which changes to D after 720 seconds.
In ΔADB
`"AB"/"DB" = tan45^circ`
`"AB"/"DB" = 1`
DB = AB
In ΔABC
`"AB"/"BC" = tan 30^circ`
`"AB"/"BD + DC" = 1/sqrt(3)`
`"AB"sqrt(3) = "BD + DC"`
`"AB"sqrt(3) = "AB + DC"`
`"DC" = "AB"sqrt(3) - "AB" = "AB"(sqrt(3) - 1)`
Time taken by car to travel DC distance (i.e `"AB"(sqrt(3) - 1`)) = 720 seconds
Time taken by car to travel DB distance (i.e. AB)
= `720/("AB"(sqrt(3) - 1)) xx "AB" = 720/((sqrt(3) - 1)) xx (sqrt(3) + 1)/(sqrt(3) + 1)`
= `(720(sqrt(3) + 1))/2 = 360(sqrt(3) + 1) = 360 xx 2.732 = 983.52`
Thus , the required time taken is 983.52 seconds = 984 seconds = 16 mins 24 secs.
APPEARS IN
संबंधित प्रश्न
Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
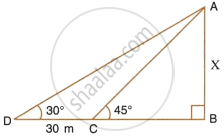
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of a light house in a horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer corrected to the nearest metre.
An aeroplane takes off at angle of `30^circ` with the ground . Find the height of the aeroplane above the ground when it has travelled 386m without changing direction .
The height of an observation tower is 180m above sea level. A ship coming towards the tower is observed at an angle of depression of 30°. Calculate the distance of the boat from the foot of the observation tower.
Two persons standing on opposite sides of a tower observe the angles of elevation of the top of the tower to be 60° and 50° respectively. Find the distance between them, if the height of the tower is 80m.
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
