Advertisements
Advertisements
प्रश्न
A man on the top of a tower observes that a car is moving directly at a uniform speed towards it. If it takes 720 seconds for the angle of depression to change from 30° to 45°, how soon will the car reach the observation tower?
उत्तर
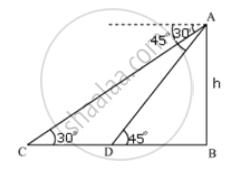
Let AB be the tower .
Initial position of car is C , which changes to D after 720 seconds.
In ΔADB
`"AB"/"DB" = tan45^circ`
`"AB"/"DB" = 1`
DB = AB
In ΔABC
`"AB"/"BC" = tan 30^circ`
`"AB"/"BD + DC" = 1/sqrt(3)`
`"AB"sqrt(3) = "BD + DC"`
`"AB"sqrt(3) = "AB + DC"`
`"DC" = "AB"sqrt(3) - "AB" = "AB"(sqrt(3) - 1)`
Time taken by car to travel DC distance (i.e `"AB"(sqrt(3) - 1`)) = 720 seconds
Time taken by car to travel DB distance (i.e. AB)
= `720/("AB"(sqrt(3) - 1)) xx "AB" = 720/((sqrt(3) - 1)) xx (sqrt(3) + 1)/(sqrt(3) + 1)`
= `(720(sqrt(3) + 1))/2 = 360(sqrt(3) + 1) = 360 xx 2.732 = 983.52`
Thus , the required time taken is 983.52 seconds = 984 seconds = 16 mins 24 secs.
APPEARS IN
संबंधित प्रश्न
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
Find AD.

A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
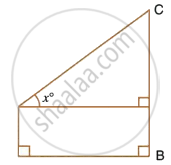
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = `2/5`.
Calculate :
- the distance AB in metres;
- angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
Two-person standing on the same side of a tower in a straight line with it measures the angle of elevation of the top of the tower as 25° and 50° respectively. If the height of the tower is 70 m find the distance between the two-person.
