Advertisements
Advertisements
प्रश्न
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
उत्तर १
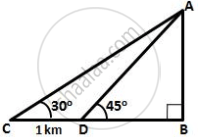
Let AB be the hill of height 'h' km and C and D be two consecutive stones such that CD = 1 km, ∠ACB = 30° and ∠ADB = 45°
In ΔABD,
`(AB)/(BD) = tan 45^circ = 1`
`=>` BD = h
In ΔABC,
`(AB)/(BC) = tan 30^circ`
`=> h/(BC) = 1/sqrt(3)`
`=> h/(h + 1) = 1/sqrt(3)`
`=> h = 1/(sqrt(3) - 1)`
= `(sqrt(3) + 1)/2`
= `2.732/2`
= 1.366 km
∴ BD = 1.366 km
BC = BD + DC
= 1.366 + 1
= 2.366 km
Hence, the two stone are at a distance of 1.366 km and 2.366 km from the foot of the hill.
उत्तर २
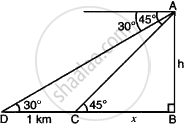
Let AB be hill of which B is foot of hill and D and C are two consecutive Km stones.
∴ DC = 1 km = 1000 m
In right-angled ΔABC,
`tan 45^circ = (AB)/(BC)`
`1 = h/x`
x = h ...(i)
In right-angled ΔABD,
`tan 30^circ = (AB)/(BD)`
`1/sqrt(3) = h/(x + 1000)`
`x + 1000 = hsqrt(3)` ...(ii)
But from equation (i), x = h,
∴ `x + 1000 = xsqrt(3)`
`x(sqrt(3) - 1) = 1000`
`x = 1000/(sqrt(3) - 1) xx (sqrt(3) + 1)/(sqrt(3) + 1)`
`x = (1000(sqrt(3) + 1))/(2)`
`x = 500(sqrt(3) + 1)`
x = 500 × 2.732
x = 1366 metre
x = 1.366 km
∴ 1st km stone is 1.366 km and 2nd km stone is 2.366 km from foot of hill.
संबंधित प्रश्न
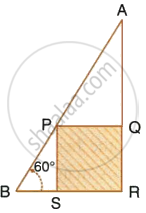
In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
A vertical tower stand on horizontel plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and that of the top of flagstaff is β. Prove that the height of the tower is
`(h tan alpha)/(tan beta - tan alpha)`
A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
The string of a kite is 150 m long and it makes an angle of 60° with the horizontal. Find the height of the kite from the ground.
An aeroplane at an altitude of 250 m observes the angle of depression of two Boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
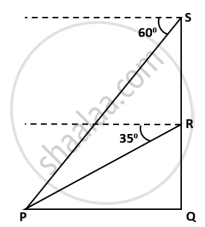
A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions is 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.