Advertisements
Advertisements
Question
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
Solution 1
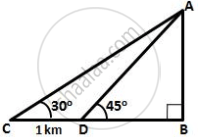
Let AB be the hill of height 'h' km and C and D be two consecutive stones such that CD = 1 km, ∠ACB = 30° and ∠ADB = 45°
In ΔABD,
`(AB)/(BD) = tan 45^circ = 1`
`=>` BD = h
In ΔABC,
`(AB)/(BC) = tan 30^circ`
`=> h/(BC) = 1/sqrt(3)`
`=> h/(h + 1) = 1/sqrt(3)`
`=> h = 1/(sqrt(3) - 1)`
= `(sqrt(3) + 1)/2`
= `2.732/2`
= 1.366 km
∴ BD = 1.366 km
BC = BD + DC
= 1.366 + 1
= 2.366 km
Hence, the two stone are at a distance of 1.366 km and 2.366 km from the foot of the hill.
Solution 2
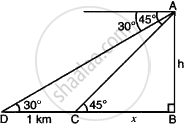
Let AB be hill of which B is foot of hill and D and C are two consecutive Km stones.
∴ DC = 1 km = 1000 m
In right-angled ΔABC,
`tan 45^circ = (AB)/(BC)`
`1 = h/x`
x = h ...(i)
In right-angled ΔABD,
`tan 30^circ = (AB)/(BD)`
`1/sqrt(3) = h/(x + 1000)`
`x + 1000 = hsqrt(3)` ...(ii)
But from equation (i), x = h,
∴ `x + 1000 = xsqrt(3)`
`x(sqrt(3) - 1) = 1000`
`x = 1000/(sqrt(3) - 1) xx (sqrt(3) + 1)/(sqrt(3) + 1)`
`x = (1000(sqrt(3) + 1))/(2)`
`x = 500(sqrt(3) + 1)`
x = 500 × 2.732
x = 1366 metre
x = 1.366 km
∴ 1st km stone is 1.366 km and 2nd km stone is 2.366 km from foot of hill.
RELATED QUESTIONS
In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to 30o and 60o respectively. Find:
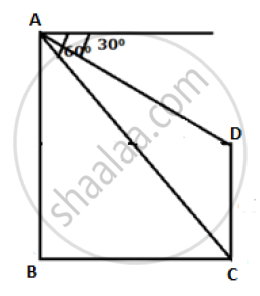
1) The horizontal distance between AB and CD.
2) The height of the lamp post.
Two persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30° and 38° respectively. Find the distance between them, if the height of the tower is 50 m.
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff.
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
An aeroplane takes off at angle of `30^circ` with the ground . Find the height of the aeroplane above the ground when it has travelled 386m without changing direction .
An aeroplane at an altitude of 200 m observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river.
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
An aeroplane at an altitude of 250 m observes the angle of depression of two Boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
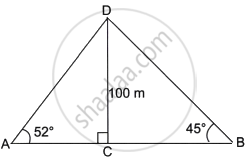
The angle of elevation of the top of a 100 m high tree from two points A and B on the opposite side of the tree are 52° and 45° respectively. Find the distance AB, to the nearest metre.