Advertisements
Advertisements
Question
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
Solution
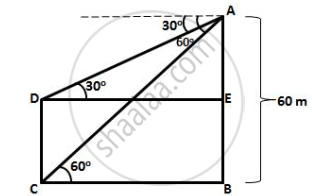
Let AB be the cliff and CD be the tower.
Here AB = 60 m, ∠ADE = 30° and ∠ACB = 60°
In ΔABC,
`(AB)/(BC) = tan 60^circ = sqrt(3)`
`=> BC = (60)/(sqrt(3))`
In ΔADE,
`(AE)/(DE) = tan 30^circ`
`=>` AE = DE tan 30°
= `60/(sqrt(3)) xx 1/sqrt(3)` ...[∵ DE = BC]
= 20 m
∴ CD = EB
= AB – AE
= (60 – 20)
= 40 m
Hence, height of the tower is 40 m.
APPEARS IN
RELATED QUESTIONS
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate ‘x’.
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
Find AD.

In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
The shadow of a vertical tower on a level ground increases by 10 m when the altitude of the sun changes from 45° to 30°. Find the height of the tower, correct to two decimal places.
