Advertisements
Advertisements
Question
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
Solution
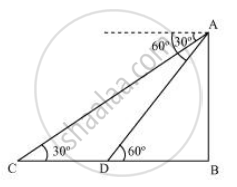
Let AB be the diff. Then , AB = 450 m
Initial position of boat is C , which changes to D after 3 minutes.
In ΔADB
`"AB"/"DB" = tan60^circ`
`450/"DB" = sqrt(3)`
`"DB" = 450/sqrt(3)`
In ΔABC
`"AB"/"BC" = tan30^circ`
`450/("BD + DC") = 1/sqrt(3)`
`450sqrt(3) = "BD + DC"`
`450sqrt(3) = 450/sqrt(3) + "DC"`
`"DC" = 450sqrt(3) - 450/(sqrt(3)) = 450(sqrt(3) - 1/sqrt(3))`
= `900/sqrt(3) = 900/sqrt(3) xx sqrt(3)/sqrt(3) = 300sqrt(3)`
Time taken by car to travel DC distance (`"i.e.,"300sqrt(3)`) = 3 minutes
Time taken by car to travel DB distance `("i.e". 450/sqrt(3))`
= `3/(300sqrt(3)) xx 450/sqrt(3) = 450/300 = 1.5`
Thus , the time it will take to reach the shore is 1 min 30 secs.
Speed of the boat = `"Distance"/"Time"`
= `(300sqrt(3))/3 = 100sqrt(3) = 100 xx 1.732 = 173.2` m/min
= `173.2/60` m/sec = 2.9 m/sec
APPEARS IN
RELATED QUESTIONS
Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32°24′ with the pole and when it is turned to rest against another pole, it makes angle 32°24′ with the road. Calculate the width of the road.
A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole is 60° and the angle of elevation of the top of the pole, as seen from the foot of the tower is 30°. Find:
- the height of the tower;
- the horizontal distance between the pole and the tower.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
Two persons standing on opposite sides of a tower observe the angles of elevation of the top of the tower to be 60° and 50° respectively. Find the distance between them, if the height of the tower is 80m.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
A man is standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
An aeroplane at an altitude of 250 m observes the angle of depression of two Boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions is 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.