Advertisements
Advertisements
Question
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
Solution
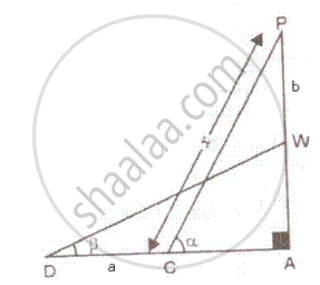
Let CP and DW be the two position of the ladder such that CP = DW = x (say).
CD = a , PW = b, ∠ACP = α and ∠ADW = β
In ΔAPC,
`"AC"/"CP" = cos α ⇒ "AC" = "x" cosα"` ....(i)
In ΔADW,
`"AD"/"DW" = cos β ⇒ ("AC + CD")/("DW") = cos β`
⇒ `("x" cosα + a)/"x" = cos β` [using (i)]
⇒ `"x" = a/(cos β - cos α)` ...(ii)
Again in ΔAPC, `"AP"/"CP" = sin α`
⇒ `"AP" = "x" sin α = (a sinα)/((cos β - cosα))` ....(iii) [Using (ii)]
Again in ΔADW, `"AW"/"DW" = sin β`
⇒ `"AW" = "x" sin β = (a sin β)/((cos β - cos α))` ...(iv)
Now , PW = AP - AW
⇒ `"b" = ((asinα)/(cosβ -cosα)) - ((asinβ)/(cosβ - cosα)) = (a(sinα -sinβ))/((cosβ - cosα))`
⇒ `a/b = (cosβ - cosα)/(sinα -sinβ)`
Hence proved.
APPEARS IN
RELATED QUESTIONS
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45°, (ii) 60°. Find the height of the tower in each case.
From the top of a light house 100 m high, the angles of depression of two ships are observed as 48° and 36° respectively. Find the distance between the two ships (in the nearest metre) if:
- the ships are on the same side of the light house,
- the ships are on the opposite sides of the light house.
A vertical tower stand on horizontel plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and that of the top of flagstaff is β. Prove that the height of the tower is
`(h tan alpha)/(tan beta - tan alpha)`
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
Find the length of the shadow cast by a tree 60 m high when the sun's altitude is `30^circ`.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
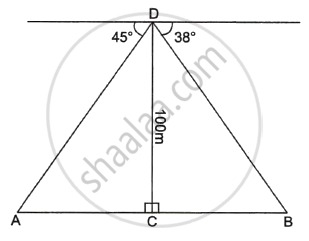
From the top of a tower 100 m high a man observes the angles of depression of two ships A and B, on opposite sides of the tower as 45° and 38° respectively. If the foot of the tower and the ships are in the same horizontal line find the distance between the two ships A and B to the nearest metre.
(Use Mathematical Tabels for this question)