Advertisements
Advertisements
Question
A vertical tower stand on horizontel plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and that of the top of flagstaff is β. Prove that the height of the tower is
`(h tan alpha)/(tan beta - tan alpha)`
Solution
Let height of tower AB = x
Height of flag staff CA = h.
Which makes the angles of elevation β and α at D.
In right ΔADB, we have
`tan alpha = (AB)/(DB) = x/(DB)`
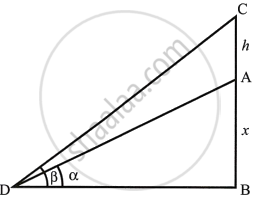
∴ `DB = x/(tan alpha)` ...(i)
And in right ΔCDB, we have
`tan beta = (CB)/(DB) = (h + x)/(DB)`
∴ `DB = (h + x)/(tan beta)` ...(ii)
From (i) and (ii)
`(h + x)/tan beta = x/tan alpha`
`\implies` h tan α + x tan α = x tan β
`\implies` h tan α = x tan β – x tan α
`\implies` h tan α = x (tan β – tan α)
∴ `x = (h tan alpha)/(tan beta - tan alpha)`
Hence required height of tower = `(h tan alpha)/(tan beta - tan alpha)`
APPEARS IN
RELATED QUESTIONS
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
Find AD.

A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
The shadow of a vertical tower on a level ground increases by 10 m when the altitude of the sun changes from 45° to 30°. Find the height of the tower, correct to two decimal places.
A man on the top of vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower? (Give your answer correct to nearest seconds).
An aeroplane when 3,000 meters high passes vertically above another aeroplane at an instance when their angles of elevation at the same observation point are 60° and 45° respectively. How many meters higher is the one than the other?
The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
A vertical tower standing on a horizontal plane is surmounted by a vertical flagstaff. At a point 100 m away from the foot of the tower, the angle of elevation of the top and bottom of the flagstaff are 54° and 42° respectively. Find the height of the flagstaff. Give your answer correct to nearest metre.

