Advertisements
Advertisements
Question
The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
Solution
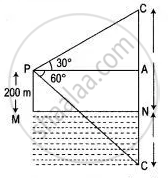
Let P be the point of observation and C, the position of cloud. CN ⊥ from C on the surface of the lake and C' be the reflection of the cloud in the lake so that
CN = NC' = x (say)
Then, PM = 200 m
∴ AN = MP = 200 m
CA = CN - AN = ( x - 200 ) m
C'A = NC' + AN = ( x + 200 ) m
Let, PA = y m
Then in right angled ΔPAC,
⇒ `(CA)/(PA) = tan 30°`
⇒ `(x - 200)/y = 1/sqrt3`
⇒ y = √3( x - 200) ....(i)
Also, in right angled ΔC'AP,
⇒ `(C'A)/(PA) = tan 60°`
⇒ `(x + 200)/y = sqrt3`
⇒ x + 200 = √3y
⇒ y = `( x + 200)/sqrt3` .....(ii)
From (i) and (ii),
⇒ `(x + 200)/sqrt3 = sqrt3(x - 200)`
⇒ x + 200 = 3( x - 200)
⇒ x + 200 = 3x - 600
⇒ 2x = 800
⇒ x = 400
Hence, the height of the cloud = 400 m.
APPEARS IN
RELATED QUESTIONS
A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m and the string makes an angle 30° with the ground.
Calculate BC.
Find the length of the shadow cast by a tree 60 m high when the sun's altitude is `30^circ`.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
An observer, 1.5m tall, is 28.5m away from a tower 30m high. Determine the angle of elevation of the top of the tower from his eye.
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.
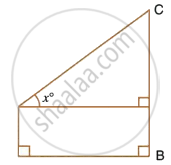
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = `2/5`.
Calculate :
- the distance AB in metres;
- angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.