Advertisements
Advertisements
प्रश्न
The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
उत्तर
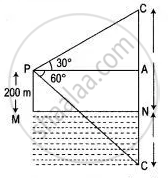
Let P be the point of observation and C, the position of cloud. CN ⊥ from C on the surface of the lake and C' be the reflection of the cloud in the lake so that
CN = NC' = x (say)
Then, PM = 200 m
∴ AN = MP = 200 m
CA = CN - AN = ( x - 200 ) m
C'A = NC' + AN = ( x + 200 ) m
Let, PA = y m
Then in right angled ΔPAC,
⇒ `(CA)/(PA) = tan 30°`
⇒ `(x - 200)/y = 1/sqrt3`
⇒ y = √3( x - 200) ....(i)
Also, in right angled ΔC'AP,
⇒ `(C'A)/(PA) = tan 60°`
⇒ `(x + 200)/y = sqrt3`
⇒ x + 200 = √3y
⇒ y = `( x + 200)/sqrt3` .....(ii)
From (i) and (ii),
⇒ `(x + 200)/sqrt3 = sqrt3(x - 200)`
⇒ x + 200 = 3( x - 200)
⇒ x + 200 = 3x - 600
⇒ 2x = 800
⇒ x = 400
Hence, the height of the cloud = 400 m.
APPEARS IN
संबंधित प्रश्न
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate ‘x’.
A man observes the angle of elevation of the top of a building to be 30o. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60o. Find the height of the building correct to the nearest metre.
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff.
Find the height of a tree when it is found that on walking away from it 20 m, in a horizontal line through its base, the elevation of its top changes from 60° to 30°.
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of a light house in a horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer corrected to the nearest metre.
The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
The angles of depression and elevation of the top of a 12m high building from the top and the bottom of a tower are 60° and 30° respectively. Find the height of the tower, and its distance from the building.
An aeroplane at an altitude of 200 m observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river.
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

