Advertisements
Advertisements
प्रश्न
A man observes the angle of elevation of the top of a building to be 30o. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60o. Find the height of the building correct to the nearest metre.
उत्तर
Let the height of the building be AB = h and BC = x
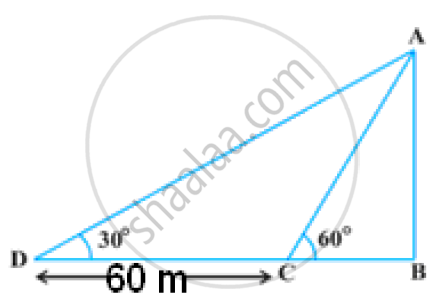
In ΔABC
`tan 60^@ = h/x`
`=> xsqrt3 = h` ...(1)
In ΔADB
`tan 30^@ = h/(x + 60)`
`=> 1/sqrt3 = h/(x + 60)`
`=> x + 60 = hsqrt3` ... (2)
From (1)and (2)
`=> x + 60 = xsqrt3.sqrt3`
`=> x= 30`
Thus `h = 3sqrt3 = 51.96m ~~ "52 metre"`
APPEARS IN
संबंधित प्रश्न
Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32°24′ with the pole and when it is turned to rest against another pole, it makes angle 32°24′ with the road. Calculate the width of the road.
A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole is 60° and the angle of elevation of the top of the pole, as seen from the foot of the tower is 30°. Find:
- the height of the tower;
- the horizontal distance between the pole and the tower.
An aeroplane, at an altitude of 250 m, observes the angles of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. If the boats are on the opposite sides of the aeroplane, find the width of the river. Write the answer correct to the nearest whole number.
The top of a ladder reaches a pcint on the wall 5 m above the ground. If the foot of the ladder makes an angle of 30° with the ground, find the length of the ladder.
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
The angles of depression of two cars on a straight road as observed from the top of a 42m high building are 60° and 75° respectively. Find the distance between the cars if they are on opposite sides of the building.
The angle of elevation of a tower from a point 200 m from its base is θ, when `tan θ = 2/5`. The angle of elevation of this tower from a point 120m from its base is `Φ`. Calculate the height of tower and the value of `Φ`.
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
