Advertisements
Advertisements
Question
A man observes the angle of elevation of the top of a building to be 30o. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60o. Find the height of the building correct to the nearest metre.
Solution
Let the height of the building be AB = h and BC = x
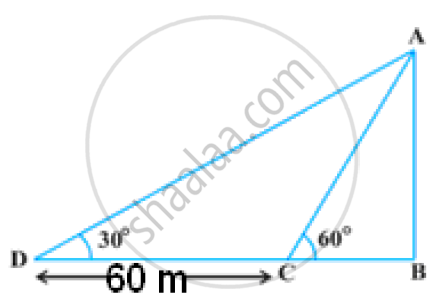
In ΔABC
`tan 60^@ = h/x`
`=> xsqrt3 = h` ...(1)
In ΔADB
`tan 30^@ = h/(x + 60)`
`=> 1/sqrt3 = h/(x + 60)`
`=> x + 60 = hsqrt3` ... (2)
From (1)and (2)
`=> x + 60 = xsqrt3.sqrt3`
`=> x= 30`
Thus `h = 3sqrt3 = 51.96m ~~ "52 metre"`
APPEARS IN
RELATED QUESTIONS
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

Calculate AB.

The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
The angles of depression and elevation of the top of a 12m high building from the top and the bottom of a tower are 60° and 30° respectively. Find the height of the tower, and its distance from the building.
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
Two persons standing on opposite sides of a tower observe the angles of elevation of the top of the tower to be 60° and 50° respectively. Find the distance between them, if the height of the tower is 80m.
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
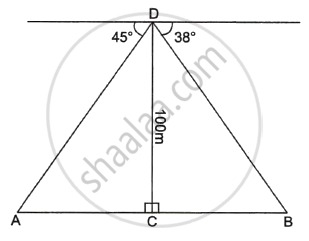
From the top of a tower 100 m high a man observes the angles of depression of two ships A and B, on opposite sides of the tower as 45° and 38° respectively. If the foot of the tower and the ships are in the same horizontal line find the distance between the two ships A and B to the nearest metre.
(Use Mathematical Tabels for this question)