Advertisements
Advertisements
Question
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
Solution
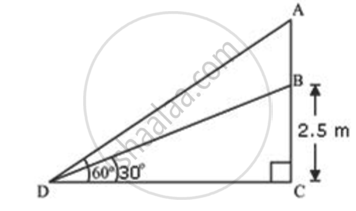
Let AB be the flagstaff, BC be the pole and D be the point on ground from where elevation angles are measured.
In ΔBCD
`"BC"/"CD" = tan 30^circ`
`"BC"/"CD" = 1/sqrt(3)`
`sqrt(3)"BC" = "CD"` ....(1)
In ΔACD
`("AB + BC")/"CD" = tan 60^circ`
`("AB + BC")/"CD" = sqrt(3)`
`"AB" + 2.5 = "CD"sqrt(3) = 3"BC"` [Using (1)]
`"AB" + 2.5 = 3 xx 2.5`
`"AB" + 2.5 = 7.5`
AB = 5
Thus , the height of the flagstaff is 5 m.
APPEARS IN
RELATED QUESTIONS
An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
A ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of 68° with the ground. Find the height, upto which the ladder reaches.
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff.
The angle of elevation of the top of a tower is observed to be 60°. At a point, 30 m vertically above the first point of observation, the elevation is found to be 45°. Find:
- the height of the tower,
- its horizontal distance from the points of observation.
The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7 meters. At a point in a plane, the angle of elevation of the bottom and the top of the flagstaff are respectively 30° and 60°. Find the height of the tower.
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
