Advertisements
Advertisements
Question
The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
Solution
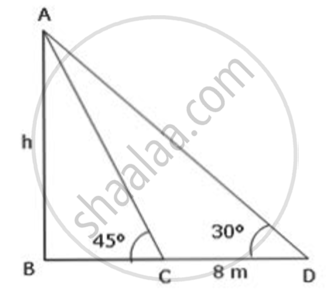
Let the height of the statue (AB) be h.
In ΔABC,
`tan45^circ = "AB"/"BC"`
⇒ BC = h
In ΔABD,
`tan30^circ = "AB"/"BD"`
`1/sqrt(3) = "AB"/("BC + CD")`
h + 8 = `sqrt(3)`h (∵ BC = h)
⇒ `"h"(sqrt(3)` - 1) = 8
⇒ h = `8/(sqrt(3) - 1) × (sqrt(3) + 1)/(sqrt(3) + 1)`
⇒ h = `(8(sqrt(3) + 1))/2 = 4(sqrt(3) + 1) = 4 xx 2.732 = 10.928 ≈ 10.93`
Thus, the height of the tower is 10. 93 m.
APPEARS IN
RELATED QUESTIONS
The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
A vertical tower stand on horizontel plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and that of the top of flagstaff is β. Prove that the height of the tower is
`(h tan alpha)/(tan beta - tan alpha)`
An aeroplane, at an altitude of 250 m, observes the angles of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. If the boats are on the opposite sides of the aeroplane, find the width of the river. Write the answer correct to the nearest whole number.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
The top of a palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9m from the foot of the tree. Find the original height of the palm tree.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
From a lighthouse, the angles of depression of two ships on opposite sides of the lighthouse were observed to be 30° and 45°. If the height of the lighthouse is 90 metres and the line joining the two ships passes through the foot of the lighthouse, find the distance between the two ships, correct to two decimal places.
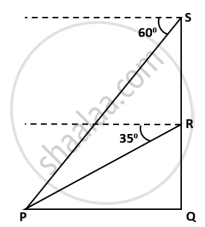
A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions is 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.