Advertisements
Advertisements
Question
The top of a palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9m from the foot of the tree. Find the original height of the palm tree.
Solution
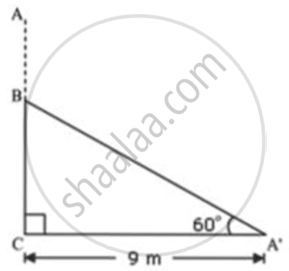
Let AC was original tree. It was broken into two parts. The broken part A' B is making 60° with ground.
In ΔA'BC
`"BC"/"A'C" = tan 60^circ`
`"BC"/9 = sqrt(3)`
`BC = 9sqrt(3)`
`"A'C"/"A'B" = cos 60^circ`
`9/"A'B" = 1/2`
`A'B = 18`
Height of tree = A'B + BC
= `9sqrt(3) + 18 = 9 × 1.732 + 18 = 15.588 + 18 = 33.588`
Hence , the height of tree was 33.588 m = 33.6 m (approximately).
APPEARS IN
RELATED QUESTIONS
Two persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30° and 38° respectively. Find the distance between them, if the height of the tower is 50 m.
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
Of the two trees are on either side of a river, one of them is 50m high. From the top of this tree the angles of depression of the top and the foot of the other tree are 30° and 60° respectively. Find the width of the river and the height of the other tree.
A man on the top of a tower observes a truck at an angle of depression ∝ where `∝ = 1/sqrt(5)` and sees that it is moving towards the base of the tower. Ten minutes later, the angle of depression of the truck is found to `β = sqrt(5)`. Assuming that the truck moves at a uniform speed, determine how much more ti me it will take to each the base of the tower?
The string of a kite is 150 m long and it makes an angle of 60° with the horizontal. Find the height of the kite from the ground.
In figures, find the length CF.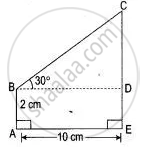
From a lighthouse, the angles of depression of two ships on opposite sides of the lighthouse were observed to be 30° and 45°. If the height of the lighthouse is 90 metres and the line joining the two ships passes through the foot of the lighthouse, find the distance between the two ships, correct to two decimal places.
The shadow of a vertical tower on a level ground increases by 10 m when the altitude of the sun changes from 45° to 30°. Find the height of the tower, correct to two decimal places.
The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
