Question

Two persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30° and 38° respectively. Find the distance between them, if the height of the tower is 50 m.

Answer 1

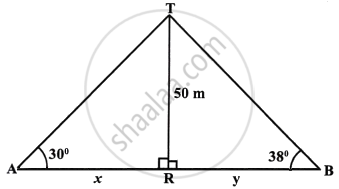
Two persons A and B are standing on the opposite side of the tower TR and height of tower TR = 50 m and angles of elevation with A and B are 30° and 38° respectively.

Let AR = x and RB = y

Now in right ΔTAR, we have

${\displaystyle \tan \theta =\frac{TR}{AR}}$

${\displaystyle \Rightarrow {\tan 30}^{\circ }=\frac{50}{x}}$

${\displaystyle \Rightarrow \frac{1}{\sqrt{3}}=\frac{50}{x}}$

∴ ${\displaystyle x=50\sqrt{3}=86.60 m}$

Again in right ΔTRB, we have

${\displaystyle {\tan 38}^{\circ }=\frac{50}{y}}$

${\displaystyle \Rightarrow }$ y tan 38° = 50

${\displaystyle y=\frac{50}{{\tan 38}^{\circ }}}$

= ${\displaystyle \frac{50}{0.7813}}$

= 63.99

or 64.00 m   ...(i)

∴ Distance between A and B

= x + y

= 86.60 + 64.00

= 150.6 m