Advertisements
Advertisements
प्रश्न
Two persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30° and 38° respectively. Find the distance between them, if the height of the tower is 50 m.
उत्तर
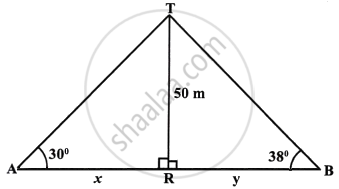
Two persons A and B are standing on the opposite side of the tower TR and height of tower TR = 50 m and angles of elevation with A and B are 30° and 38° respectively.
Let AR = x and RB = y
Now in right ΔTAR, we have
`tan theta = (TR)/(AR)`
`=> tan 30^circ = 50/x`
`=> 1/sqrt(3) = 50/x `
∴ `x = 50sqrt(3) = 86.60 m`
Again in right ΔTRB, we have
`tan 38^circ = 50/y`
`=>` y tan 38° = 50
`y = 50/tan 38^circ`
= `50/0.7813`
= 63.99
or 64.00 m ...(i)
∴ Distance between A and B
= x + y
= 86.60 + 64.00
= 150.6 m
APPEARS IN
संबंधित प्रश्न
A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45°, (ii) 60°. Find the height of the tower in each case.
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
An aeroplane flying horizontally 1 km above the ground and going away from the observer is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°; find the uniform speed of the aeroplane in km per hour.
Find AD.

The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
A man on the top of a tower observes that a car is moving directly at a uniform speed towards it. If it takes 720 seconds for the angle of depression to change from 30° to 45°, how soon will the car reach the observation tower?
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
The shadow of a vertical tower on a level ground increases by 10 m when the altitude of the sun changes from 45° to 30°. Find the height of the tower, correct to two decimal places.
A man is standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
