Advertisements
Advertisements
प्रश्न
A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
उत्तर
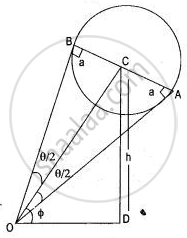
Let C be the centre of the balloon, O be the position of man's eye.
Let h be the height of the centre of the balloon.
Then, ∠AOB = θ
So, ∠BOC = ∠COA = `θ/2`
In ΔOAC,
sin θ/2 = `a/"OC"`
⇒ OC = a cosec `θ/2`
In ΔCOD,
`sin Φ = h/"OC"`
`⇒ h = OC sin Φ`
`⇒ h = a cosec θ/2 sin Φ`
`⇒ h = a sin Φ cosec θ/2`
APPEARS IN
संबंधित प्रश्न
Prove the following identities:
sin4A – cos4A = 2sin2A – 1
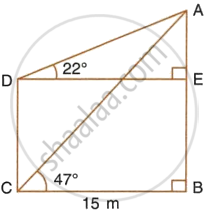
From the figure, given below, calculate the length of CD.
A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
The horizontal distance between towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60m, find the height of the first tower.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
An aeroplane when 3,000 meters high passes vertically above another aeroplane at an instance when their angles of elevation at the same observation point are 60° and 45° respectively. How many meters higher is the one than the other?
The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
