Advertisements
Advertisements
प्रश्न
Vertical tower is 20m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
उत्तर
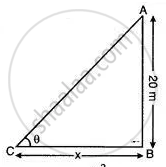
Given, cos θ = 0.53
Let the man is standing at a distance of 'x' m from the foot of the tower.
cos θ = `"BC"/"AC" = x/(sqrt(x^2 + 400))`
0.53 = `x/(sqrt(x^2 + 400))`
⇒ `(0.53)^2 = x^2/(sqrt(x^2 + 400))`
⇒ 0.2809 x2 + 112.36 = x2
⇒ x2 - 0.2809 x2 = 112.36
⇒ x2 = `(112.36)/(0.7191)`
⇒ x2 = 156.25
⇒ x = 12.5 metres
∴ The man is standing from the foot of the tower be 12.5 meter.
APPEARS IN
संबंधित प्रश्न
The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?
The radius of a circle is given as 15 cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, calculate:
- the length of AB;
- the distance of AB from the centre C.
A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole is 60° and the angle of elevation of the top of the pole, as seen from the foot of the tower is 30°. Find:
- the height of the tower;
- the horizontal distance between the pole and the tower.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

A boy is 1.54 m tall. Standing at a distance of 3m in front of a 4.54 m high wall he can just manage to see the sun. Find the angle of elevation of the sun.
Two boats approaching a light house in mid sea from opposite directions observe the angle of elevation of the top of the light house as 30° and 45° respectively. If the distance between the two boats is 150m, find the height of the light house.
The string of a kite is 150 m long and it makes an angle of 60° with the horizontal. Find the height of the kite from the ground.
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

A man on the top of vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower? (Give your answer correct to nearest seconds).
An aeroplane when 3,000 meters high passes vertically above another aeroplane at an instance when their angles of elevation at the same observation point are 60° and 45° respectively. How many meters higher is the one than the other?
