Advertisements
Advertisements
प्रश्न
The radius of a circle is given as 15 cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, calculate:
- the length of AB;
- the distance of AB from the centre C.
उत्तर
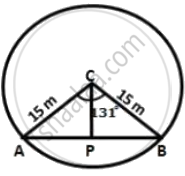
Given, CA = CB = 15 cm, ∠ACB = 131°
Drop a perpendicular CP from center C to the chord AB.
Then CP bisects ∠ACB as well as chord AB.
∴ ∠ACP = 65.5°
In ΔACP,
`(AP)/(AC) = sin(65.5^circ)`
`=>` AP = 15 × 0.91 = 13.65 cm
i. AB = 2AP
= 2 × 13.65
= 27.30 cm.
ii. CP = AP cos (65.5°)
= 15 × 0.415
= 6.22 cm.
APPEARS IN
संबंधित प्रश्न
Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32°24′ with the pole and when it is turned to rest against another pole, it makes angle 32°24′ with the road. Calculate the width of the road.
A man stands 9 m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28° and the angle of depression of the bottom of the pole is 13°. Calculate the height of the pole.
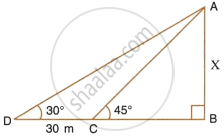
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
An aeroplane flying horizontally 1 km above the ground and going away from the observer is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°; find the uniform speed of the aeroplane in km per hour.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
From the top of a light house 96m high, the angles of depression of two ships in the river and at the same level as the base of the light house and on the same side of it, are α and β. If tan α = `1/4` and tan β = `1/7`, find the distance between the ships.
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
From a lighthouse, the angles of depression of two ships on opposite sides of the lighthouse were observed to be 30° and 45°. If the height of the lighthouse is 90 metres and the line joining the two ships passes through the foot of the lighthouse, find the distance between the two ships, correct to two decimal places.
A man is standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
