Advertisements
Advertisements
प्रश्न
An aeroplane flying horizontally 1 km above the ground and going away from the observer is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°; find the uniform speed of the aeroplane in km per hour.
उत्तर

Let A be the aeroplane and B be the observer on the ground. The vertical height will be AC = 1 km = 1000 m. After 10 seconds, let the aeroplane be at point D.
Let the speed of the aeroplane be x m/sec.
∴ CE = 10x
In ΔABC,
`(AC)/(BC) = tan 60^circ`
`=> 1000/(BC) = sqrt(3)`
`=> BC = 1000/sqrt(3)m`
In ΔBDE,
`(DE)/(BE) = tan 30^circ`
`=> BE = 1000 sqrt(3)`
∴ CE = BE – BC
`=> 10x = 1000sqrt(3) - 1000/sqrt(3)`
`=> x = 100 (sqrt(3) - 1/sqrt(3))`
= 100 × 1.154
= 115.4 m/sec
= `115.4 xx 18/5` km/hr
= 415.44 km/hr
Hence, speed of the aeroplane is 415.44 km/hr.
APPEARS IN
संबंधित प्रश्न
Evaluate without using trigonometric tables.
`2((tan 35^@)/(cot 55^@))^2 + ((cot 55^@)/(tan 35^@)) - 3((sec 40^@)/(cosec 50^@))`
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
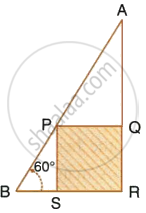
In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
A vertical pole is 90m high and the length of its shadow is `90sqrt(3)`. what is the angle of elevation of the sun ?
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
The angles of depression of two cars on a straight road as observed from the top of a 42m high building are 60° and 75° respectively. Find the distance between the cars if they are on opposite sides of the building.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

Vertical tower is 20m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
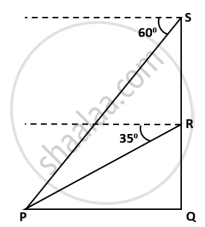
A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions is 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.