Advertisements
Advertisements
प्रश्न
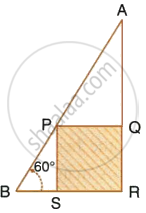
In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
उत्तर

In ΔPSB,
`(PS)/(PB) = sin 60^circ`
`=> PB = 2/sqrt(3) = 1.155 m`
In ΔAPQ,
∠APQ = 60°
∴ `(PQ)/(AP) = cos 60^circ`
`=> AP = 1/(1/2) = 2 m`
∴ AB = AP + PB
= 2 + 1.155
= 3.155 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

A man observes the angle of elevation of the top of a building to be 30o. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60o. Find the height of the building correct to the nearest metre.
The radius of a circle is given as 15 cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, calculate:
- the length of AB;
- the distance of AB from the centre C.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
The angles of depression and elevation of the top of a 12m high building from the top and the bottom of a tower are 60° and 30° respectively. Find the height of the tower, and its distance from the building.
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
In figures, find the length CF.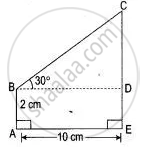
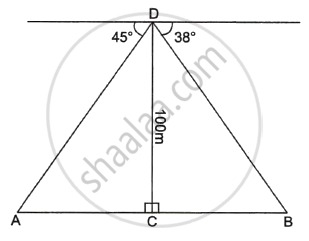
From the top of a tower 100 m high a man observes the angles of depression of two ships A and B, on opposite sides of the tower as 45° and 38° respectively. If the foot of the tower and the ships are in the same horizontal line find the distance between the two ships A and B to the nearest metre.
(Use Mathematical Tabels for this question)