Advertisements
Advertisements
प्रश्न
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
उत्तर
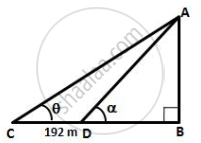
Let AB be the vertical tower and C and D be two point such that CD = 192 m. Let ∠ACB = θ and ∠ADB = α
Given, `tan theta = 5/12`
`=> (AB)/(BC) = 5/12`
`=> AB = 5/12 BC` ...(i)
Also, `tan alpha = 3/4`
`=> (AB)/(BD) = 3/4`
`=> ((5)/(12)BC)/(BD) = 3/4`
`=> (192 + BD)/(BD) = 3/4 xx 12/5`
`=>` BD = 240 m
∴ BC = (192 + 240) = 432 m
∴ By (i), `AB = 5/12 xx 432 = 180 m`
Hence, the height of the tower is 180 m.
APPEARS IN
संबंधित प्रश्न
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate ‘x’.
In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to 30o and 60o respectively. Find:
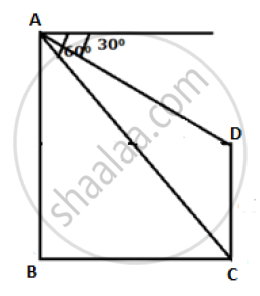
1) The horizontal distance between AB and CD.
2) The height of the lamp post.
Prove the following identities:
sin4A – cos4A = 2sin2A – 1
At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
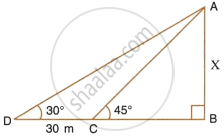
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

