Advertisements
Advertisements
प्रश्न
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
उत्तर
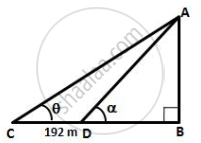
Let AB be the vertical tower and C and D be two point such that CD = 192 m. Let ∠ACB = θ and ∠ADB = α
Given, `tan theta = 5/12`
`=> (AB)/(BC) = 5/12`
`=> AB = 5/12 BC` ...(i)
Also, `tan alpha = 3/4`
`=> (AB)/(BD) = 3/4`
`=> ((5)/(12)BC)/(BD) = 3/4`
`=> (192 + BD)/(BD) = 3/4 xx 12/5`
`=>` BD = 240 m
∴ BC = (192 + 240) = 432 m
∴ By (i), `AB = 5/12 xx 432 = 180 m`
Hence, the height of the tower is 180 m.
APPEARS IN
संबंधित प्रश्न
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
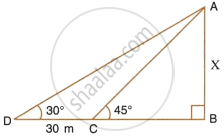
Find AD.

The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
The horizontal distance between two trees of different heights is 100m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 150m, find the height of the first tree.
The string of a kite is 150 m long and it makes an angle of 60° with the horizontal. Find the height of the kite from the ground.
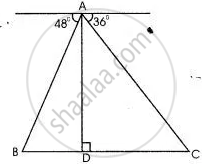
From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7 meters. At a point in a plane, the angle of elevation of the bottom and the top of the flagstaff are respectively 30° and 60°. Find the height of the tower.
