Advertisements
Advertisements
प्रश्न
The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
उत्तर
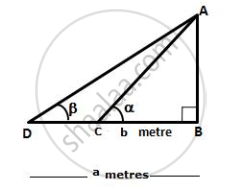
Let AB be the tower of height h metre
Let C and D be two points on the level ground such that BC = b metres, BD = a metres, ∠ACB = α and ∠ADB = β
Given, α + β = 90°
In ΔABC,
`(AB)/(BC) = tan alpha`
`=> h/b = tan alpha` ...(i)
In ΔABD,
`(AB)/(BD) = tan beta`
`=> h/a = tan (90^circ - alpha) = cot alpha` ...(ii)
Multiplying (i) by (ii), we get,
`(h/a)(h/b) = 1`
`=>` h2 = ab
∴ `h = sqrt(ab)` metre
Hence, height of the tower is `sqrt(ab)` metre.
APPEARS IN
संबंधित प्रश्न
The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?
A man stands 9 m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28° and the angle of depression of the bottom of the pole is 13°. Calculate the height of the pole.
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45°. Find the height of the first tower.
A vertical tower stand on horizontel plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and that of the top of flagstaff is β. Prove that the height of the tower is
`(h tan alpha)/(tan beta - tan alpha)`
Find the length of the shadow cast by a tree 60 m high when the sun's altitude is `30^circ`.
A kite tied to a string makes an angle of 60° with the ground. Find the perpendicular height of the kite if the length of its string is 250 m.
A ladder rests against a tree on one side of a street. The foot of the ladder makes an angle of 50° with the ground. When the ladder is turned over to rest against another tree on the other side of the street it makes an angle of 40° with the ground. If the length of the ladder is 60m, find the width of the street.
The shadow of a vertical tower on a level ground increases by 10 m when the altitude of the sun changes from 45° to 30°. Find the height of the tower, correct to two decimal places.
From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places.
An aeroplane is flying horizontally along a straight line at a height of 3000 m from the ground at a speed of 160 m/s. Find the time it would take for the angle of elevation of the plane as seen from a particular point on the ground to change from 60⁰ to 45⁰. Give your answer correct to the nearest second.
