Advertisements
Advertisements
प्रश्न
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45°. Find the height of the first tower.
उत्तर
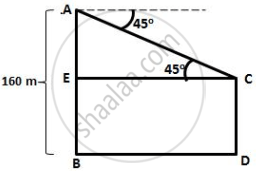
Let AB and CD be the two towers.
The height of the first tower is AB = 160 m
The horizontal distance between the two towers is BD = 75 m
And the angle of depression of the first tower as seen from the top of the second tower is ∠ACE = 45°
In ΔACE,
`(AE)/(EC) = tan 45^circ = 1`
`=>` AE = EC = BD = 75 m
∴ CD = EB
= AB – AE
= (160 – 75)
= 85 m
Hence, height of the other tower is 85 m.
APPEARS IN
संबंधित प्रश्न
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
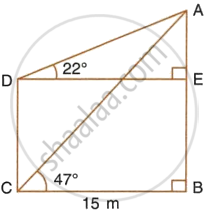
From the figure, given below, calculate the length of CD.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
A man on the top of a tower observes a truck at an angle of depression ∝ where `∝ = 1/sqrt(5)` and sees that it is moving towards the base of the tower. Ten minutes later, the angle of depression of the truck is found to `β = sqrt(5)`. Assuming that the truck moves at a uniform speed, determine how much more ti me it will take to each the base of the tower?
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
An aeroplane when 3,000 meters high passes vertically above another aeroplane at an instance when their angles of elevation at the same observation point are 60° and 45° respectively. How many meters higher is the one than the other?
Vertical tower is 20m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
