Advertisements
Advertisements
प्रश्न
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
उत्तर १
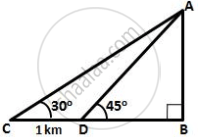
Let AB be the hill of height 'h' km and C and D be two consecutive stones such that CD = 1 km, ∠ACB = 30° and ∠ADB = 45°
In ΔABD,
`(AB)/(BD) = tan 45^circ = 1`
`=>` BD = h
In ΔABC,
`(AB)/(BC) = tan 30^circ`
`=> h/(BC) = 1/sqrt(3)`
`=> h/(h + 1) = 1/sqrt(3)`
`=> h = 1/(sqrt(3) - 1)`
= `(sqrt(3) + 1)/2`
= `2.732/2`
= 1.366 km
∴ BD = 1.366 km
BC = BD + DC
= 1.366 + 1
= 2.366 km
Hence, the two stone are at a distance of 1.366 km and 2.366 km from the foot of the hill.
उत्तर २
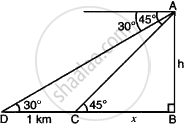
Let AB be hill of which B is foot of hill and D and C are two consecutive Km stones.
∴ DC = 1 km = 1000 m
In right-angled ΔABC,
`tan 45^circ = (AB)/(BC)`
`1 = h/x`
x = h ...(i)
In right-angled ΔABD,
`tan 30^circ = (AB)/(BD)`
`1/sqrt(3) = h/(x + 1000)`
`x + 1000 = hsqrt(3)` ...(ii)
But from equation (i), x = h,
∴ `x + 1000 = xsqrt(3)`
`x(sqrt(3) - 1) = 1000`
`x = 1000/(sqrt(3) - 1) xx (sqrt(3) + 1)/(sqrt(3) + 1)`
`x = (1000(sqrt(3) + 1))/(2)`
`x = 500(sqrt(3) + 1)`
x = 500 × 2.732
x = 1366 metre
x = 1.366 km
∴ 1st km stone is 1.366 km and 2nd km stone is 2.366 km from foot of hill.
संबंधित प्रश्न
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

Two persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30° and 38° respectively. Find the distance between them, if the height of the tower is 50 m.
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
The horizontal distance between two trees of different heights is 100m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 150m, find the height of the first tree.
Of the two trees are on either side of a river, one of them is 50m high. From the top of this tree the angles of depression of the top and the foot of the other tree are 30° and 60° respectively. Find the width of the river and the height of the other tree.
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
The shadow of a vertical tower on a level ground increases by 10 m when the altitude of the sun changes from 45° to 30°. Find the height of the tower, correct to two decimal places.
From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places.
