Advertisements
Advertisements
प्रश्न
A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60°. When he moves 50 m away from the bank, he finds the angle of elevation to be 30°.
Calculate :
- the width of the river;
- the height of the tree.
उत्तर १

Let AB be the tree and AC be the width of the river.
Let D be a point such that CD = 50 m.
Given that ∠BCA = 60° and ∠BDA = 30°
In ΔBAD,
`(BA)/(AD) = tan 30^circ`
`=> BA = (AD)/sqrt(3)` ...(i)
In ΔBAC,
`(BA)/(AC) = tan 60^circ`
`=> BA = ACsqrt(3)` ...(ii)
From (i) and (ii), we get
`(AD)/(sqrt(3)) = ACsqrt(3)`
`=>` (50 + AC) = 3AC
∴ AC = 25 m
Thus, width of the river is 25 m.
From (ii),
BA = 25 × 1.732 = 43.3 m
Hence, height of the tree is 43.3 m.
उत्तर २
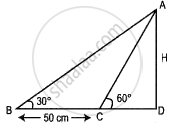
Let H be the height of the tree
Let height of the tree be H meter.
In right-angled ΔACD,
`tan 60^circ = H/(CD)`
`sqrt(3) = H/(CD)`
∴ `CD = H/sqrt(3)` ...(i)
In right-angled ΔABD,
`tan 30^circ = H/(BD)`
∴ `1/sqrt(3) = H/(BD)`
`BD = sqrt(3)H` ...(ii)
BD – CD = 50
`(sqrt(3)H)/1 - H/sqrt(3) = 50` ...(Using (i) and (ii))
∴ `(3H - H )/sqrt(3) = 50`
∴ `2H = 50sqrt(3)`
or `H = (50sqrt(3))/2 = 25sqrt(3)`
H = 43.3 m
i. The width of the river `CD = (25sqrt(3))/sqrt(3) = 25 m`
ii. The height of the tree H = 43.3 m.
संबंधित प्रश्न
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
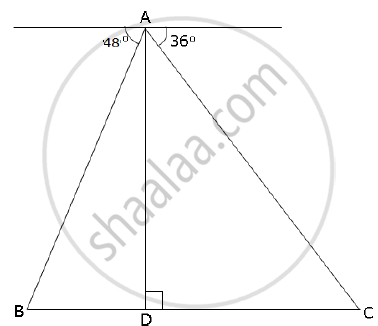
From the top of a lighthouse, 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
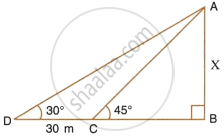
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
The top of a ladder reaches a pcint on the wall 5 m above the ground. If the foot of the ladder makes an angle of 30° with the ground, find the length of the ladder.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

Vertical tower is 20m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
