Advertisements
Advertisements
प्रश्न
A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60°. When he moves 50 m away from the bank, he finds the angle of elevation to be 30°.
Calculate :
- the width of the river;
- the height of the tree.
उत्तर १

Let AB be the tree and AC be the width of the river.
Let D be a point such that CD = 50 m.
Given that ∠BCA = 60° and ∠BDA = 30°
In ΔBAD,
`(BA)/(AD) = tan 30^circ`
`=> BA = (AD)/sqrt(3)` ...(i)
In ΔBAC,
`(BA)/(AC) = tan 60^circ`
`=> BA = ACsqrt(3)` ...(ii)
From (i) and (ii), we get
`(AD)/(sqrt(3)) = ACsqrt(3)`
`=>` (50 + AC) = 3AC
∴ AC = 25 m
Thus, width of the river is 25 m.
From (ii),
BA = 25 × 1.732 = 43.3 m
Hence, height of the tree is 43.3 m.
उत्तर २
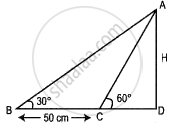
Let H be the height of the tree
Let height of the tree be H meter.
In right-angled ΔACD,
`tan 60^circ = H/(CD)`
`sqrt(3) = H/(CD)`
∴ `CD = H/sqrt(3)` ...(i)
In right-angled ΔABD,
`tan 30^circ = H/(BD)`
∴ `1/sqrt(3) = H/(BD)`
`BD = sqrt(3)H` ...(ii)
BD – CD = 50
`(sqrt(3)H)/1 - H/sqrt(3) = 50` ...(Using (i) and (ii))
∴ `(3H - H )/sqrt(3) = 50`
∴ `2H = 50sqrt(3)`
or `H = (50sqrt(3))/2 = 25sqrt(3)`
H = 43.3 m
i. The width of the river `CD = (25sqrt(3))/sqrt(3) = 25 m`
ii. The height of the tree H = 43.3 m.
संबंधित प्रश्न
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole is 60° and the angle of elevation of the top of the pole, as seen from the foot of the tower is 30°. Find:
- the height of the tower;
- the horizontal distance between the pole and the tower.
A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = `2/5`.
Calculate :
- the distance AB in metres;
- angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places.
A man is standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
