Advertisements
Advertisements
प्रश्न
Vertical tower is 20m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
उत्तर
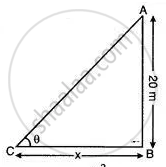
Given, cos θ = 0.53
Let the man is standing at a distance of 'x' m from the foot of the tower.
cos θ = `"BC"/"AC" = x/(sqrt(x^2 + 400))`
0.53 = `x/(sqrt(x^2 + 400))`
⇒ `(0.53)^2 = x^2/(sqrt(x^2 + 400))`
⇒ 0.2809 x2 + 112.36 = x2
⇒ x2 - 0.2809 x2 = 112.36
⇒ x2 = `(112.36)/(0.7191)`
⇒ x2 = 156.25
⇒ x = 12.5 metres
∴ The man is standing from the foot of the tower be 12.5 meter.
APPEARS IN
संबंधित प्रश्न
Evaluate without using trigonometric tables.
`2((tan 35^@)/(cot 55^@))^2 + ((cot 55^@)/(tan 35^@)) - 3((sec 40^@)/(cosec 50^@))`
A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m and the string makes an angle 30° with the ground.
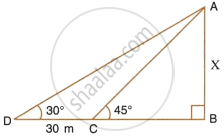
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
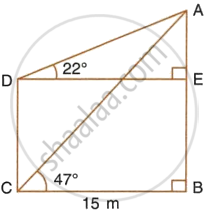
From the figure, given below, calculate the length of CD.
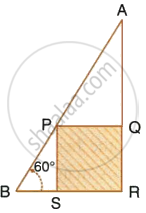
In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
A vertical pole is 90m high and the length of its shadow is `90sqrt(3)`. what is the angle of elevation of the sun ?
A ladder rests against a tree on one side of a street. The foot of the ladder makes an angle of 50° with the ground. When the ladder is turned over to rest against another tree on the other side of the street it makes an angle of 40° with the ground. If the length of the ladder is 60m, find the width of the street.
Two persons standing on opposite sides of a tower observe the angles of elevation of the top of the tower to be 60° and 50° respectively. Find the distance between them, if the height of the tower is 80m.
The angle of elevation of a tower from a point 200 m from its base is θ, when `tan θ = 2/5`. The angle of elevation of this tower from a point 120m from its base is `Φ`. Calculate the height of tower and the value of `Φ`.
If the angle of elevation of a cloud from a point h m above a lake is α, and the angle of depression of its reflection in the lake be β, prove that distance of the cloud from the point of observation is `("2h"secα)/(tanα - tanβ)`.
