Advertisements
Advertisements
प्रश्न
If the angle of elevation of a cloud from a point h m above a lake is α, and the angle of depression of its reflection in the lake be β, prove that distance of the cloud from the point of observation is `("2h"secα)/(tanα - tanβ)`.
उत्तर
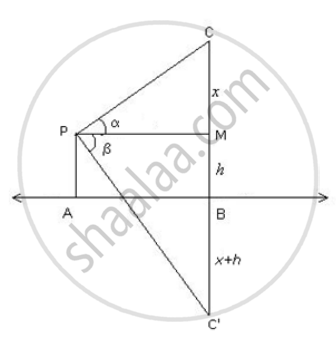
Let AB be the surface of the lake and let P be an point of observation such that AP = h meters . Let c be the position of the cloud and C' be its reflection in the lake . Then ∠CPM = α and ∠MPC = β. Let CM = x.
Then , CB = CM + MB = CM + PA = x + h
In ΔCPM,
tan α = `"CM"/"PM"`
⇒ `tan α = "x"/"AB"` [∵ PM = AB]
⇒ AB = x cotα ...(1)
In ΔPMC',
`tanβ = (C'M)/(PM)`
⇒ `tanβ = ("x" + "2h")/"AB"`
⇒ AB = (x + 2h)cotβ ....(2)
From (1) and (2),
x cotα = (x + 2h) cot β
⇒ `"x"(1/tanα - 1/tanβ) = "2h"/tanβ`
⇒ `"x"((tanβ - tanα) /(tanα tanβ)) = "2h"/tanβ`
⇒ x = `("2h"tanα)/(tanβ- tanα)`
Again, in Δ CPM,
`sin α = "CM"/"PC"` = `"x"/("PC")`
⇒ PC = `"x"/sin α`
⇒ `"PC" = ("2h"tanα)/(tanβ - tanα) xx 1/sin α`
⇒ `"PC" = ("2h"secα)/(tanβ - tanα)`
Hence , the distance of the cloud from the point of observation is `("2h"secα)/(tanβ - tanα)`.
APPEARS IN
संबंधित प्रश्न
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is 30° and 24° respectively.
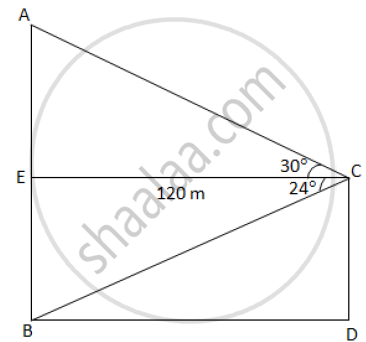
Find the height of the two towers. Give your answer correct to 3 significant figures
From the top of a light house 100 m high, the angles of depression of two ships are observed as 48° and 36° respectively. Find the distance between the two ships (in the nearest metre) if:
- the ships are on the same side of the light house,
- the ships are on the opposite sides of the light house.
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole is 60° and the angle of elevation of the top of the pole, as seen from the foot of the tower is 30°. Find:
- the height of the tower;
- the horizontal distance between the pole and the tower.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
A vertical tow er stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the ft agstaff is 45°. Find the height of the tower.
An observer, 1.5m tall, is 28.5m away from a tower 30m high. Determine the angle of elevation of the top of the tower from his eye.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7 meters. At a point in a plane, the angle of elevation of the bottom and the top of the flagstaff are respectively 30° and 60°. Find the height of the tower.
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
