Advertisements
Advertisements
प्रश्न
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7 meters. At a point in a plane, the angle of elevation of the bottom and the top of the flagstaff are respectively 30° and 60°. Find the height of the tower.
उत्तर
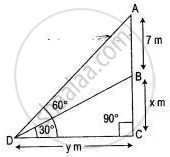
Let the height of the tower be x m and distance DC = y m.
∴ AB = height of flagstaff = 7 m
Now in right-angled Δ BCD,
`"BC"/"CD" = tan 30°`
∴ `x/y = 1/sqrt3`
⇒ y = √3x ....(i)
Also, in right angled Δ ACD,
`"AC"/"CD" = tan 60°`
⇒ `(x + 7)/y = sqrt3`
⇒ x + 7 = √3y
⇒ x + 7 = 3(√3 x) ...(from (i))
⇒ x + 7 = 3x
⇒ 2x = 7
⇒ x = `7/2` = 3.5 m
APPEARS IN
संबंधित प्रश्न
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is 30° and 24° respectively.
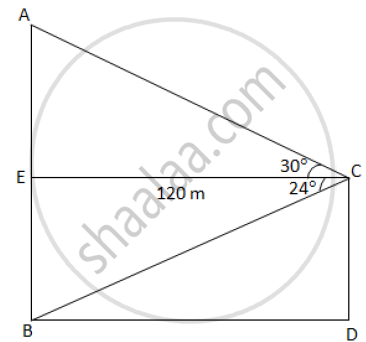
Find the height of the two towers. Give your answer correct to 3 significant figures
A man observes the angle of elevation of the top of a building to be 30o. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60o. Find the height of the building correct to the nearest metre.
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
Calculate AB.

At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
The top of a ladder reaches a pcint on the wall 5 m above the ground. If the foot of the ladder makes an angle of 30° with the ground, find the length of the ladder.
From a point 10 m above the ground , the angle of elevation of the top of a tower is α and the angle of depression is β . If tan α = `5/2` and tan β = `1/4` , calculate the height of the tower to the nearest metre .
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

