Advertisements
Advertisements
प्रश्न
From a point 10 m above the ground , the angle of elevation of the top of a tower is α and the angle of depression is β . If tan α = `5/2` and tan β = `1/4` , calculate the height of the tower to the nearest metre .
उत्तर
Let AD be the tower and B be the point of observation.
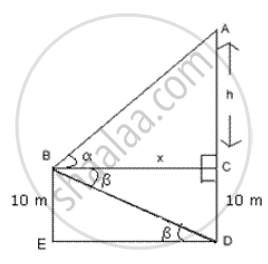
In ΔABC,
tan ∝ = `"AC"/"BC"`
⇒ `"h"/"x" = 5/2` ....(1)
In ΔBED,
`tanβ = "BE"/"ED"`
⇒ `1/4 = 10/"x"`
⇒ x = 40
From (1),
h = 100
∴ Height of the tower = h + 10 = 100 + 10 = 110 m
APPEARS IN
संबंधित प्रश्न
A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45°, (ii) 60°. Find the height of the tower in each case.
Two climbers are at points A and B on a vertical cliff face. To an observer C, 40 m from the foot of the cliff, on the level ground, A is at an elevation of 48° and B of 57°. What is the distance between the climbers?
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of a light house in a horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer corrected to the nearest metre.
The angles of depression of two cars on a straight road as observed from the top of a 42m high building are 60° and 75° respectively. Find the distance between the cars if they are on opposite sides of the building.
From the top of a light house 96m high, the angles of depression of two ships in the river and at the same level as the base of the light house and on the same side of it, are α and β. If tan α = `1/4` and tan β = `1/7`, find the distance between the ships.
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
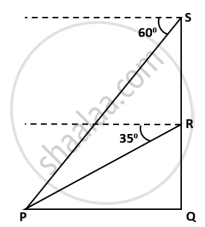
A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions is 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.