Advertisements
Advertisements
Question
From a point 10 m above the ground , the angle of elevation of the top of a tower is α and the angle of depression is β . If tan α = `5/2` and tan β = `1/4` , calculate the height of the tower to the nearest metre .
Solution
Let AD be the tower and B be the point of observation.
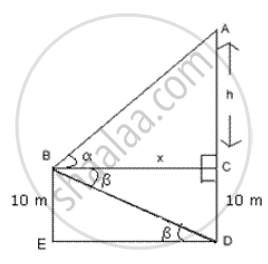
In ΔABC,
tan ∝ = `"AC"/"BC"`
⇒ `"h"/"x" = 5/2` ....(1)
In ΔBED,
`tanβ = "BE"/"ED"`
⇒ `1/4 = 10/"x"`
⇒ x = 40
From (1),
h = 100
∴ Height of the tower = h + 10 = 100 + 10 = 110 m
APPEARS IN
RELATED QUESTIONS
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?
The angle of elevation of the top of an unfinished tower from a point at a distance of 80 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32°24′ with the pole and when it is turned to rest against another pole, it makes angle 32°24′ with the road. Calculate the width of the road.
A man in a boat rowing away from a lighthouse 150 m high, takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 45°. Find the speed of the boat.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
A vertical tow er stands on a horizontal plane and is surmounted by a flagstaff of height 7m. From a point on the plane the angle of elevation of the bottom of the flagstaff is 30° and that of the top of the ft agstaff is 45°. Find the height of the tower.
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° from two observing points 100 m apart to his right. Find the height from which he falls and the distance of the point where he falls on the ground from the nearest observation pcint.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7 meters. At a point in a plane, the angle of elevation of the bottom and the top of the flagstaff are respectively 30° and 60°. Find the height of the tower.
