Advertisements
Advertisements
Question
A man in a boat rowing away from a lighthouse 150 m high, takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 45°. Find the speed of the boat.
Solution
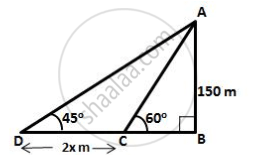
Let AB be the lighthouse and C and D be the two positions of the boat such that AB = 150 m, ∠ADB = 45° and ∠ACB = 60°.
Let speed of the boat be x metre per minute.
Therefore, CD = 2x m;
In ΔADB,
`(AB)/(DB) = tan 45^circ`
`=>` BD = 150 m
In ΔABC,
`(AB)/(BC) = tan 60^circ = sqrt(3)`
`=> 150/(BC)= sqrt(3)`
`=> BC = 150/ sqrt(3)`
= `150/1.732`
= 86.605 m
∴ CD = BD – BC
= 150 – 86.605
= 63.395 m
`=>` 2x = 63.395
`=> x = 63.395/2`
= 31.6975 m/min
= `31.6975/60` m/sec
= 0.53 m/sec
Hence, the speed of the boat is 0.53 m/sec
APPEARS IN
RELATED QUESTIONS
A man observes the angle of elevation of the top of a building to be 30o. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60o. Find the height of the building correct to the nearest metre.
A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m and the string makes an angle 30° with the ground.
Two climbers are at points A and B on a vertical cliff face. To an observer C, 40 m from the foot of the cliff, on the level ground, A is at an elevation of 48° and B of 57°. What is the distance between the climbers?
Find AD.

A vertical tower stand on horizontel plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and that of the top of flagstaff is β. Prove that the height of the tower is
`(h tan alpha)/(tan beta - tan alpha)`
The top of a palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9m from the foot of the tree. Find the original height of the palm tree.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
A man on the top of a tower observes that a car is moving directly at a uniform speed towards it. If it takes 720 seconds for the angle of depression to change from 30° to 45°, how soon will the car reach the observation tower?
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
