Advertisements
Advertisements
Question
A man on a cliff observes a boat, at an angle of depression 30°, which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depression of the boat is found to be 60°. Assuming that the boat sails at a uniform speed, determine:
- how much more time it will take to reach the shore?
- the speed of the boat in metre per second, if the height of the cliff is 500 m.
Solution
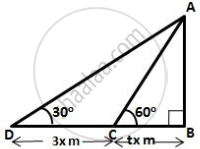
Let AB be the cliff and C and D be the two position of the boat such that ∠ADE = 30° and ∠ACB = 60°
Let speed of the boat be X metre per minute and let the boat reach the shore after t minutes more.
In ΔABC,
`(AB)/(BC) = tan 60^circ = sqrt(3)`
`=> h/(tx) = sqrt(3)`
In ΔADB,
`(AB)/(DB) = tan 30^circ`
`=> (h)/(3x + tx ) = 1/sqrt(3)`
`=> (sqrt(3)t)/(3 + t) = 1/sqrt(3)`
`=>` 3t = 3 + t
∴ t = `3/2` = 1.5 minute
Also, if h = 500 m, then
` (500)/(1.5 x)= sqrt(3)`
`=> x = (500)/(1.5 xx 1.732)`
= 192.455 metre per minute
= 3.21 m/sec
Hence, the boat takes an extra 1.5 minutes to reach the shore.
And if the height of cliff is 500 m, the speed of the boat is 3.21 m/sec
APPEARS IN
RELATED QUESTIONS
Prove the following identities:
sin4A – cos4A = 2sin2A – 1
Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32°24′ with the pole and when it is turned to rest against another pole, it makes angle 32°24′ with the road. Calculate the width of the road.
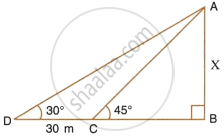
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60°. When he moves 50 m away from the bank, he finds the angle of elevation to be 30°.
Calculate :
- the width of the river;
- the height of the tree.
In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
A ladder rests against a tree on one side of a street. The foot of the ladder makes an angle of 50° with the ground. When the ladder is turned over to rest against another tree on the other side of the street it makes an angle of 40° with the ground. If the length of the ladder is 60m, find the width of the street.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
A man on the deck of a ship is 10 m above water level. He observes that the angle of elevation of the top of a cliff is 42° and the angle of depression of the base is 20°. Calculate the distance of the cliff from the ship and the height of the cliff.
Two-person standing on the same side of a tower in a straight line with it measures the angle of elevation of the top of the tower as 25° and 50° respectively. If the height of the tower is 70 m find the distance between the two-person.
