Advertisements
Advertisements
Question
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
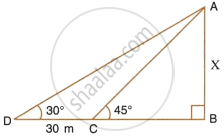
Solution
In ΔABC, we have
`tan 45^circ = (AB)/(CB) = X/(CB)` ...`[∵ tan theta = "Perpendicular"/"Base"]`
`1 = X/(CB)`
`\implies` CB = X ...(i)
Again in ΔADB, we have
`tan 30^circ = (AB)/(DB) = X/(DB)`
`\implies 1/sqrt(3) = X/(DB)`
∴ `DB = sqrt(3) xx X` ...(ii)
But DB = DC + CB
∴ `sqrt(3)X = 30 + X`
`\implies sqrt(3)X - X = 30`
`\implies X(sqrt(3) - 1) = 30`
`\implies X = 30/(sqrt(3) - 1)m`
∴ `X = (30(sqrt(3) + 1))/((sqrt(3) - 1)(sqrt(3) + 1))`
= `(30(sqrt(3) + 1))/(3 - 1)m`
= `(30(sqrt(3) + 1))/2`
= 15 (1.732 + 1) m.
= 15 × 2.732
= 40.98 m.
APPEARS IN
RELATED QUESTIONS
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is 30° and 24° respectively.
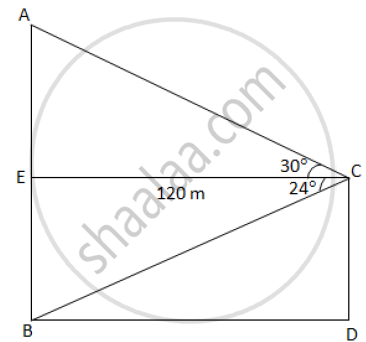
Find the height of the two towers. Give your answer correct to 3 significant figures
A man stands 9 m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28° and the angle of depression of the bottom of the pole is 13°. Calculate the height of the pole.
An aeroplane, at an altitude of 250 m, observes the angles of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. If the boats are on the opposite sides of the aeroplane, find the width of the river. Write the answer correct to the nearest whole number.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

Two persons standing on opposite sides of a tower observe the angles of elevation of the top of the tower to be 60° and 50° respectively. Find the distance between them, if the height of the tower is 80m.
The angle of elevation of a tower from a point in line with its base is `45^circ` . On moving 20m towards the tower , the angle of elevation changes to `60^circ` . Find the height of the tower.
A man on the top of a tower observes that a car is moving directly at a uniform speed towards it. If it takes 720 seconds for the angle of depression to change from 30° to 45°, how soon will the car reach the observation tower?
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
The angle of elevation of an aeroplane from a point on the ground is 45°. After 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a height of 3000 m, find the speed of the aeroplane.
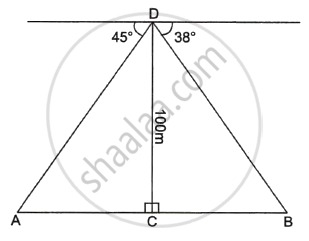
From the top of a tower 100 m high a man observes the angles of depression of two ships A and B, on opposite sides of the tower as 45° and 38° respectively. If the foot of the tower and the ships are in the same horizontal line find the distance between the two ships A and B to the nearest metre.
(Use Mathematical Tabels for this question)