Advertisements
Advertisements
Question
Two persons standing on opposite sides of a tower observe the angles of elevation of the top of the tower to be 60° and 50° respectively. Find the distance between them, if the height of the tower is 80m.
Solution
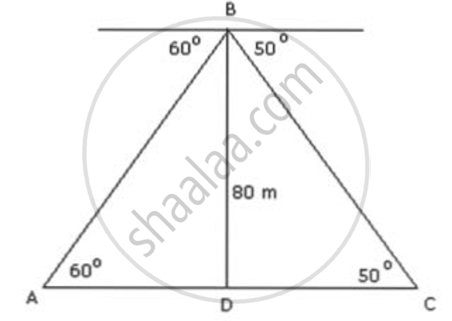
Let the position of the two persons be A and C. Let BD be the tower of height 80 m.
In ΔBAD,
`tan60^circ = "BD"/"AD"`
⇒ `sqrt(3) = 80/"AD"`
⇒ `"AD" = 80/sqrt(3)`
⇒ AD = `(80sqrt(3))/3 = (80 xx 1.732)/3` = 46.19 ...(1)
In ΔBDC,
`tan50^circ = "BD"/"DC"`
⇒ `1.1918 = 80/"DC"`
⇒ `"DC" = 80/1.1918 = 67.13` ....(2)
:. AC = AD + DC = 46.19 m + 67 .13 m = 113.32 m
Thus, the horizontal distance between the two persons is 113. 32 m.
APPEARS IN
RELATED QUESTIONS
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of a light house in a horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer corrected to the nearest metre.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
An aeroplane takes off at angle of `30^circ` with the ground . Find the height of the aeroplane above the ground when it has travelled 386m without changing direction .
The top of a ladder reaches a pcint on the wall 5 m above the ground. If the foot of the ladder makes an angle of 30° with the ground, find the length of the ladder.
A ladder rests against a tree on one side of a street. The foot of the ladder makes an angle of 50° with the ground. When the ladder is turned over to rest against another tree on the other side of the street it makes an angle of 40° with the ground. If the length of the ladder is 60m, find the width of the street.
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
