Advertisements
Advertisements
प्रश्न
Two persons standing on opposite sides of a tower observe the angles of elevation of the top of the tower to be 60° and 50° respectively. Find the distance between them, if the height of the tower is 80m.
उत्तर
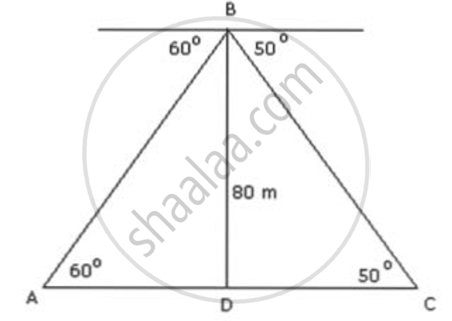
Let the position of the two persons be A and C. Let BD be the tower of height 80 m.
In ΔBAD,
`tan60^circ = "BD"/"AD"`
⇒ `sqrt(3) = 80/"AD"`
⇒ `"AD" = 80/sqrt(3)`
⇒ AD = `(80sqrt(3))/3 = (80 xx 1.732)/3` = 46.19 ...(1)
In ΔBDC,
`tan50^circ = "BD"/"DC"`
⇒ `1.1918 = 80/"DC"`
⇒ `"DC" = 80/1.1918 = 67.13` ....(2)
:. AC = AD + DC = 46.19 m + 67 .13 m = 113.32 m
Thus, the horizontal distance between the two persons is 113. 32 m.
APPEARS IN
संबंधित प्रश्न
Find AD.

The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
The angle of elevation of a tower from a point 200 m from its base is θ, when `tan θ = 2/5`. The angle of elevation of this tower from a point 120m from its base is `Φ`. Calculate the height of tower and the value of `Φ`.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
An aeroplane at an altitude of 250 m observes the angle of depression of two Boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
