Advertisements
Advertisements
प्रश्न
An aeroplane at an altitude of 250 m observes the angle of depression of two Boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
उत्तर
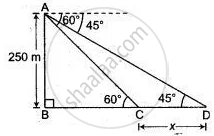
Let the width of the river CD be x,
In ΔABC,
tan 60° = `"AB"/"BC"`
√3 = `250/"BC"`
BC = `250/sqrt3 xx sqrt3/sqrt3`
BC = `(250/3)sqrt3` .....(i)
In Δ ABD,
tan 45° = `"AB"/"BD"`
⇒ AB = BD = 250 ....(ii)
∴ BD = BC + CD
∴ 250 = `(250/3) sqrt3 + x` ....(using (i) and (ii))
∴ x = 250 - `(250/3) xx 1.732`
∴ x = 250 - 83.33 x 1.732
∴ x = 250 - 144.33
∴ x = 105.67 m
∴ x = 106 m .....(to the nearest whole numbers)
Thus, width of the river is 106 m.
APPEARS IN
संबंधित प्रश्न
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

Evaluate without using trigonometric tables.
`2((tan 35^@)/(cot 55^@))^2 + ((cot 55^@)/(tan 35^@)) - 3((sec 40^@)/(cosec 50^@))`
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
A man on a cliff observes a boat, at an angle of depression 30°, which is sailing towards the shore to the point immediately beneath him. Three minutes later, the angle of depression of the boat is found to be 60°. Assuming that the boat sails at a uniform speed, determine:
- how much more time it will take to reach the shore?
- the speed of the boat in metre per second, if the height of the cliff is 500 m.
Find AD.

A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
The angle of elevation of a tower from a point 200 m from its base is θ, when `tan θ = 2/5`. The angle of elevation of this tower from a point 120m from its base is `Φ`. Calculate the height of tower and the value of `Φ`.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
