Advertisements
Advertisements
प्रश्न
An aeroplane at an altitude of 250 m observes the angle of depression of two Boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
उत्तर
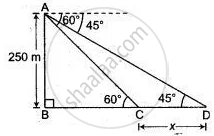
Let the width of the river CD be x,
In ΔABC,
tan 60° = `"AB"/"BC"`
√3 = `250/"BC"`
BC = `250/sqrt3 xx sqrt3/sqrt3`
BC = `(250/3)sqrt3` .....(i)
In Δ ABD,
tan 45° = `"AB"/"BD"`
⇒ AB = BD = 250 ....(ii)
∴ BD = BC + CD
∴ 250 = `(250/3) sqrt3 + x` ....(using (i) and (ii))
∴ x = 250 - `(250/3) xx 1.732`
∴ x = 250 - 83.33 x 1.732
∴ x = 250 - 144.33
∴ x = 105.67 m
∴ x = 106 m .....(to the nearest whole numbers)
Thus, width of the river is 106 m.
APPEARS IN
संबंधित प्रश्न
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

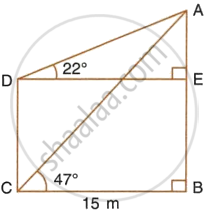
From the figure, given below, calculate the length of CD.
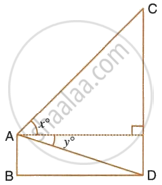
From a window A, 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan `x^circ = 5/2` and the angle of depression of the foot D of the tower is y°, where tan `y^circ = 1/4`. Calculate the height CD of the tower in metres.
A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
The angles of elevation of the top of a tower from two points A and B at a distance of a and b respectively from the base and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)`.
