Advertisements
Advertisements
प्रश्न
The angles of elevation of the top of a tower from two points A and B at a distance of a and b respectively from the base and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)`.
उत्तर
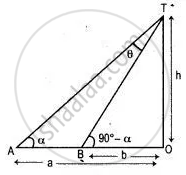
Let the height of the tower 'OT' = h.
Let O be the base of the tower.
Let A and B be two points on the same line through the base such that
OA = a, OB = b.
∵ The angles at A and B are complementary.
∴ ∠TAO = α
then ∠TBO = 90° - α
In right-angled ΔOAT,
tan α = `"OT"/"OA" = h/a` .....(i)
In right-angled ΔOBT,
tan(90° - α) = `"OT"/"OB" = h/b`
cot α = h/b` .....(ii)
Multiplying (i) and (ii), we have
tan α cot α = `h/a xx h/b = h^2/(ab)`
⇒ 1 = `h^2/(ab)`
⇒ h2 = ab
⇒ h = `sqrtab`
Hence, the height of the tower = `sqrtab`.
APPEARS IN
संबंधित प्रश्न
Prove the following identities:
sin4A – cos4A = 2sin2A – 1
The angle of elevation of the top of a tower, from a point on the ground and at a distance of 160 m from its foot, is found to be 60°. Find the height of the tower.
Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32°24′ with the pole and when it is turned to rest against another pole, it makes angle 32°24′ with the road. Calculate the width of the road.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
Find the length of the shadow cast by a tree 60 m high when the sun's altitude is `30^circ`.
A kite tied to a string makes an angle of 60° with the ground. Find the perpendicular height of the kite if the length of its string is 250 m.
The topmost branch of a tree is tied with a string attached to a pole in the ground. The length of this string Is 200m and it makes an angle of 45° with the ground. Find the distance of the pole to which the string is tied from the base of the tree.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

