Advertisements
Advertisements
प्रश्न
An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
उत्तर
Case 1: When the boats are on same side of the observation point.
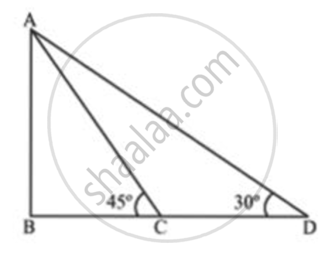
Let the position of the two ships be C and D. Let A be the point of observation.
AB = 500 m
In ΔBAC,
`tan45^circ = "AB"/"BC"`
⇒ `1 = 500/"BC"`
⇒ BC = 500 ....(1)
In ΔABD,
`tan30^circ = "AB"/"BD"`
⇒ `1/sqrt(3) = 500/"BD"`
⇒ `"BD" = 500sqrt(3)` ...(2)
From (1) and (2),
`"CD" = "BD" - "BC" = 500(sqrt(3) - 1) = 500 xx 0.732 = 366`
Thus, in this case, the distance between the boats is 366 m.
Case 2: When the boats are on different side of the observation point.
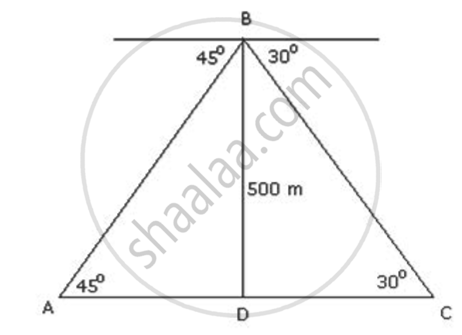
Let the position of the two ships be A and C. Let B be the point of observation.
In ΔBAD,
`tan45^circ = "BD"/"AD"`
⇒ `1 = 500/"AD"`
⇒ AD = 500 ....(1)
In ΔBDC,
`tan30^circ = "BD"/"DC"`
⇒ `1/sqrt(3) = 500/"DC"`
⇒ `"DC" = 500sqrt(3)` ....(2)
From (1) and (2),
`"AC" = "AD" + "DC" = 500 (1 + sqrt(3)) = 500 xx 2.732 = 1366`
Thus, in this case, the distance between the boats is 1366 m.
APPEARS IN
संबंधित प्रश्न
The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?
At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find:
- the height of the tree, correct to 2 decimal places,
- the width of the river.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find:
- the height of the tower, if the height of the pole is 20 m;
- the height of the pole, if the height of the tower is 75 m.
The horizontal distance between two trees of different heights is 100m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 150m, find the height of the first tree.
The angle of elevation of a tower from a point 200 m from its base is θ, when `tan θ = 2/5`. The angle of elevation of this tower from a point 120m from its base is `Φ`. Calculate the height of tower and the value of `Φ`.
Of the two trees are on either side of a river, one of them is 50m high. From the top of this tree the angles of depression of the top and the foot of the other tree are 30° and 60° respectively. Find the width of the river and the height of the other tree.
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

