Advertisements
Advertisements
प्रश्न
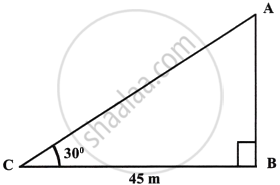
At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
उत्तर
Shadow of the tower = 45 m and angle of elevation = 30°
i. Let AB be the tower and BC is its shadow.
∴ CB = 45 m.
Now in right ΔABC,
`tan theta = (AB)/(BC)`
`\implies tan 30^circ = (AB)/45`
`\implies 1/sqrt(3) = (AB)/45`
`\implies AB = 45/sqrt(3)m`.
∴ `AB = (45 xx sqrt(3))/(sqrt(3) xx sqrt(3))`
= `(45sqrt(3))/3`
= `15sqrt(3) m`.
= 15 (1.732)
= 25.980
= 25.98 m
ii. In second case,
a. Angle of elevation = 45°
And height of tower = 25.98 m
or `15sqrt(3) m`
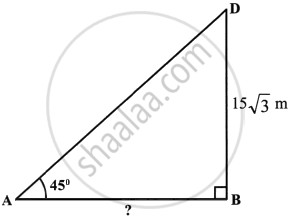
`tan 45^circ = (AB)/(DB)`
`\implies (AB)/(DB) = 1`
∴ DB = AB = 25.98 m.
b. Angle of elevation = 60°
And height of tower = 25.98 m
or `15sqrt(3) m`.
Let shadow of the tower DB = x m
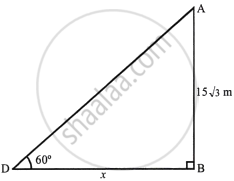
∴ `tan 60^circ = (AB)/(DB)`
`\implies sqrt(3) = (15sqrt(3))/(DB)`
`\implies DB = (15sqrt(3))/sqrt(3) = 15 m`.
Hence length of shadow = 15 m.
APPEARS IN
संबंधित प्रश्न
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
Two climbers are at points A and B on a vertical cliff face. To an observer C, 40 m from the foot of the cliff, on the level ground, A is at an elevation of 48° and B of 57°. What is the distance between the climbers?
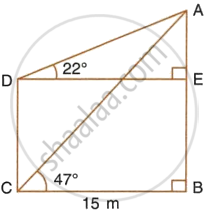
From the figure, given below, calculate the length of CD.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find:
- the height of the tree, correct to 2 decimal places,
- the width of the river.
Find AD.

A vertical tower stand on horizontel plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and that of the top of flagstaff is β. Prove that the height of the tower is
`(h tan alpha)/(tan beta - tan alpha)`
The angles of depression and elevation of the top of a 12m high building from the top and the bottom of a tower are 60° and 30° respectively. Find the height of the tower, and its distance from the building.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
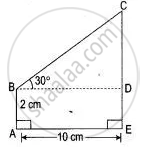
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m. The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x°, where tan x° = `2/5`.
Calculate :
- the distance AB in metres;
- angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.
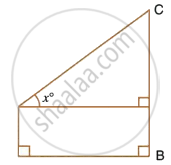
In figures, find the length CF.