Advertisements
Advertisements
प्रश्न
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
उत्तर
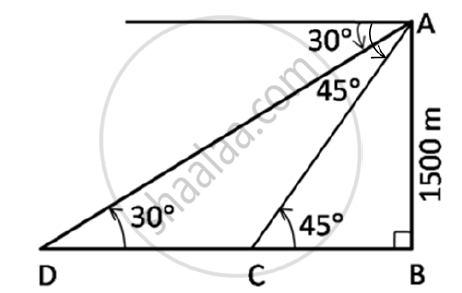
A is the aeroplane, D and C are the ships sailing towards A. Ships are sailing towards the aeroplane in the same direction.
In the figure, height AB=1500 m
To find: Distance between the ships, that is CD.
Solution:
In the right-angled ΔABC
`tan 45^@ = (AB)/(BC)`
`=> 1 = 1500/(BC)`
=> BC = 1500 m
In the right-angled ΔABD,
`tan 30^@ = (AB)/(BD)`
`=> 1/sqrt3 = 1500/(BD)`
`=> BD = 1500sqrt3`
=> BD = 1500(1.732) = 2598 m
∴ Distance between the ships = CD = BD - BC
= 2598 - 1500
= 1098 m
APPEARS IN
संबंधित प्रश्न
In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to 30o and 60o respectively. Find:
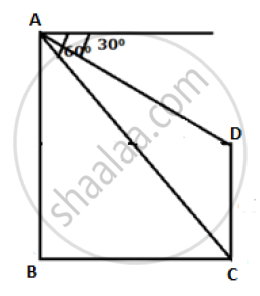
1) The horizontal distance between AB and CD.
2) The height of the lamp post.
Prove the following identities:
sin4A – cos4A = 2sin2A – 1
A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45°, (ii) 60°. Find the height of the tower in each case.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find:
- the height of the tower, if the height of the pole is 20 m;
- the height of the pole, if the height of the tower is 75 m.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
The height of an observation tower is 180m above sea level. A ship coming towards the tower is observed at an angle of depression of 30°. Calculate the distance of the boat from the foot of the observation tower.
A boy is 1.54 m tall. Standing at a distance of 3m in front of a 4.54 m high wall he can just manage to see the sun. Find the angle of elevation of the sun.
If the angle of elevation of a cloud from a point h m above a lake is α, and the angle of depression of its reflection in the lake be β, prove that distance of the cloud from the point of observation is `("2h"secα)/(tanα - tanβ)`.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
An aeroplane when 3,000 meters high passes vertically above another aeroplane at an instance when their angles of elevation at the same observation point are 60° and 45° respectively. How many meters higher is the one than the other?
