Advertisements
Advertisements
प्रश्न
In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to 30o and 60o respectively. Find:
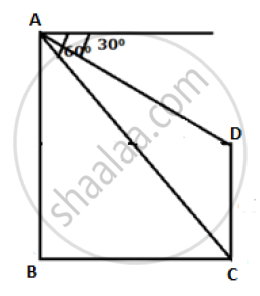
1) The horizontal distance between AB and CD.
2) The height of the lamp post.
उत्तर
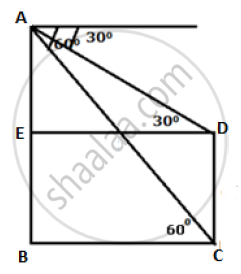
1) In ΔABC
`tan 60^@ = (AB)/(BC)`
`=> sqrt3 = 60/"BC"`
`=> BC = 60/sqrt3 = 60/sqrt3 xx sqrt3/sqrt3 = 20sqrt3 = 20 xx 1.732` = 34.64 m
2) Since BEDC is a rectangle,
`ED = BC = 20sqrt3` m
In ΔAED,
`tan 30^@ = "AE"/"ED"`
`=> 1/sqrt3 = "AE"/(20sqrt3)`
`=> AE = 20 m`
∴ Height of the lamp post = BE = AB - AE = 60 - 20 = 40 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a tower is observed to be 60°. At a point, 30 m vertically above the first point of observation, the elevation is found to be 45°. Find:
- the height of the tower,
- its horizontal distance from the points of observation.
Calculate BC.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
Find the length of the shadow cast by a tree 60 m high when the sun's altitude is `30^circ`.
The top of a palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9m from the foot of the tree. Find the original height of the palm tree.
An aeroplane at an altitude of 200 m observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
A man on the deck of a ship is 10 m above water level. He observes that the angle of elevation of the top of a cliff is 42° and the angle of depression of the base is 20°. Calculate the distance of the cliff from the ship and the height of the cliff.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7 meters. At a point in a plane, the angle of elevation of the bottom and the top of the flagstaff are respectively 30° and 60°. Find the height of the tower.
