Advertisements
Advertisements
Question
In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to 30o and 60o respectively. Find:
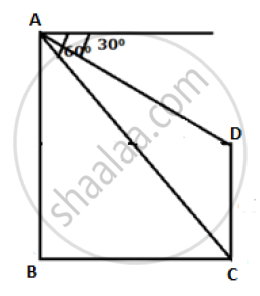
1) The horizontal distance between AB and CD.
2) The height of the lamp post.
Solution
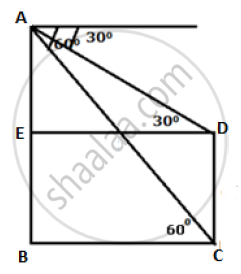
1) In ΔABC
`tan 60^@ = (AB)/(BC)`
`=> sqrt3 = 60/"BC"`
`=> BC = 60/sqrt3 = 60/sqrt3 xx sqrt3/sqrt3 = 20sqrt3 = 20 xx 1.732` = 34.64 m
2) Since BEDC is a rectangle,
`ED = BC = 20sqrt3` m
In ΔAED,
`tan 30^@ = "AE"/"ED"`
`=> 1/sqrt3 = "AE"/(20sqrt3)`
`=> AE = 20 m`
∴ Height of the lamp post = BE = AB - AE = 60 - 20 = 40 m
APPEARS IN
RELATED QUESTIONS
A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m and the string makes an angle 30° with the ground.
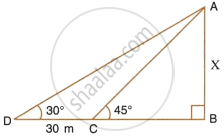
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60°. When he moves 50 m away from the bank, he finds the angle of elevation to be 30°.
Calculate :
- the width of the river;
- the height of the tree.
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
A boy is standing on the ground and flying a kite with 100m of sting at an elevation of 30°. Another boy is standing on the roof of a 10m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
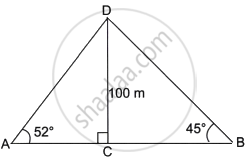
The angle of elevation of the top of a 100 m high tree from two points A and B on the opposite side of the tree are 52° and 45° respectively. Find the distance AB, to the nearest metre.